ts-ds-tool/src/binomialheap/README.md

Data structure and algorithm of TypeScript

# 二项堆 BinomialHeap\<T>

二项堆是是二项树的集合或是由一组二项树组成。二项堆具有良好的性质。在O（logn）的时间内即可完成两个二项堆合并操作，所以二项堆是可合并堆，而仅仅需要O(1)的时间，二项堆即可完成插入操作。因此，基于二项堆实现的优先队列和进程调度算法有着很好的时间性能。同时由于二项树的结构特性和性质，二项树在网络优化等诸多领域也应用广泛。
![BinomialHeap](https://img-blog.csdn.net/20170220094652634)

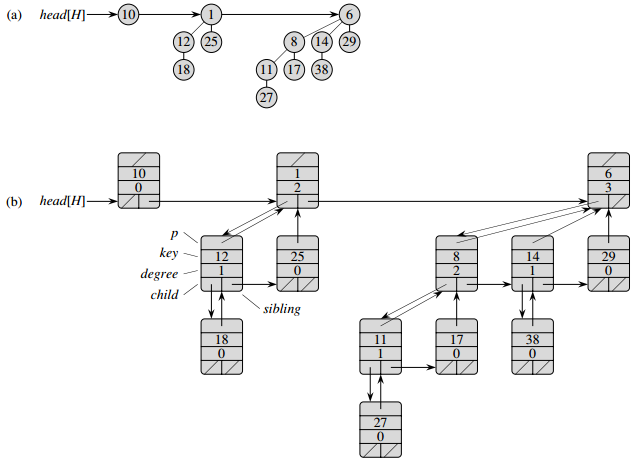
## 基本操作的API及示例
### 属性

#### 节点个数 Count
##### Count:number
``` text
实例:
const binomialHeap = new BinomialHeap();
const count = BinomialHeap.Count;
console.log(count);
//0
```

#### 头节点 Head
##### Head:LinkNode<HeapNode\<T>>
``` text
实例:
const binomialHeap = new BinomialHeap();
const head = BinomialHeap.Head;
```

###方法

#### 插入 insert
##### insert(value: T):LinkNode<HeapNode\<T>>
``` text
实例:
const binomialHeap = new BinomialHeap();
const node = binomialHeap.insert(1);
console.log(node.Value.value);
// 1
```

#### 删除最小节点 deleteExtremum
##### deleteExtremum(): T
``` text
实例:
const binomialHeap = new BinomialHeap();
binomialHeap.insert(3);
binomialHeap.insert(1);
binomialHeap.insert(2);
const value = binomialHeap.deleteExtremum();
console.log(value);
// 1
```

#### 查找最小节点 findExtremum
##### findExtremum(): T
``` text
实例:
const binomialHeap = new BinomialHeap();
binomialHeap.insert(3);
binomialHeap.insert(1);
binomialHeap.insert(2);
const value = binomialHeap.findExtremum();
console.log(value);
// 1
描述：
此方法不删除元素
```

#### 合并堆 union
##### union(heap: BinomialHeap\<T>): BinomialHeap\<T>
``` text
实例:
const binomialHeap = new BinomialHeap();
binomialHeap.insert(5);
binomialHeap.insert(4);
binomialHeap.insert(6);
const binomialHeap2 = new BinomialHeap();
binomialHeap2.insert(3);
binomialHeap2.insert(1);
binomialHeap2.insert(2);
binomialHeap.union(binomialHeap2);
console.log(binomialHeap.Count);
// 6
console.log(binomialHeap.findExtremum());
// 1
```

#### 是否为空 isEmpty
##### isEmpty(): boolean
``` text
实例:
const binomialHeap = new BinomialHeap();
const isEmpty = binomialHeap.isEmpty();
console.log(isEmpty);
// true
```

#### 清空 clear
##### clear(): void
``` text
实例:
const binomialHeap = new BinomialHeap();
binomialHeap2.insert(3);
binomialHeap2.insert(1);
binomialHeap2.insert(2);
let isEmpty = binomialHeap.isEmpty();
console.log(isEmpty);
// false

binomialHeap.clear();
isEmpty = binomialHeap.isEmpty();
console.log(isEmpty);
// true
```