timeseries-transform
Version:
timeseries-transform
52 lines (51 loc) • 25.8 kB
JSON
{
"author": {
"name": "Julien Loutre",
"email": "julien@twenty-six-medias.com",
"url": "http://www.twenty-six-medias.com/"
},
"name": "timeseries-transform",
"description": "timeseries-transform",
"version": "1.0.5",
"homepage": "https://github.com/26medias/timeseries-transform",
"licenses": [
{
"type": "MIT",
"url": "https://raw.github.com/26medias/timeseries-transform/master/LICENSE"
}
],
"keywords": [
"forecast",
"forecasting",
"timeseries",
"chart",
"charting",
"stats",
"std",
"smoothing",
"moving average",
"noise removal",
"autoregression"
],
"repository": {
"type": "git",
"url": "git://github.com/26medias/timeseries-transform.git"
},
"main": "timeseries-transform.js",
"engines": {
"node": "*"
},
"dependencies": {
"underscore": "latest"
},
"devDependencies": {},
"readmeFilename": "README.md",
"bugs": {
"url": "https://github.com/26medias/timeseries-transform/issues"
},
"readme": "# Timeseries Analysis #\r\nA chainable timeseries analysis tool.\r\n\r\nTransform your data, filter it, smooth it, remove the noise, get stats, get a preview chart of the data, ...\r\n\r\nThis lib was conceived to analyze noisy financial data but is suitable to any type of timeseries.\r\n\r\n## installation ##\r\n`npm install timeseries-analysis`\r\n\r\n`var timeseries = require(\"timeseries-analysis\");`\r\n\r\n## Note ##\r\nThis package is in early alpha, and is currently under active development.\r\n\r\nThe format or name of the methods might change in the future.\r\n\r\n## Data format ##\r\n### Loading from a timeseries with dates (default) ###\r\nThe data must be in the following format:\r\n```\r\nvar data = [\r\n [date, value],\r\n [date, value],\r\n [date, value],\r\n ...\r\n];\r\n```\r\n`date` can be in any format you want, but it is recommanded you use date value that is comaptible with a JS Date object.\r\n\r\n`value` must be a number.\r\n\r\n```\r\n// Load the data\r\nvar t = new timeseries.main(data);\r\n```\r\n\r\n### Loading from a database ###\r\nAlternatively, you can also load the data from your database:\r\n```\r\n// Unfiltered data out of MongoDB:\r\nvar data = [{\r\n \"_id\": \"53373f538126b69273039245\",\r\n \"adjClose\": 26.52,\r\n \"close\": 26.52,\r\n \"date\": \"2013-04-15T03:00:00.000Z\",\r\n \"high\": 27.48,\r\n \"low\": 26.36,\r\n \"open\": 27.16,\r\n \"symbol\": \"fb\",\r\n \"volume\": 30275400\r\n },\r\n {\r\n \"_id\": \"53373f538126b69273039246\",\r\n \"adjClose\": 26.92,\r\n \"close\": 26.92,\r\n \"date\": \"2013-04-16T03:00:00.000Z\",\r\n \"high\": 27.11,\r\n \"low\": 26.4,\r\n \"open\": 26.81,\r\n \"symbol\": \"fb\",\r\n \"volume\": 27365900\r\n },\r\n {\r\n \"_id\": \"53373f538126b69273039247\",\r\n \"adjClose\": 26.63,\r\n \"close\": 26.63,\r\n \"date\": \"2013-04-17T03:00:00.000Z\",\r\n \"high\": 27.2,\r\n \"low\": 26.39,\r\n \"open\": 26.65,\r\n \"symbol\": \"fb\",\r\n \"volume\": 26440600\r\n },\r\n ...\r\n];\r\n\r\n// Load the data\r\nvar t = new timeseries.main(timeseries.adapter.fromDB(data, {\r\n date: 'date', // Name of the property containing the Date (must be compatible with new Date(date) )\r\n value: 'close' // Name of the property containign the value. here we'll use the \"close\" price.\r\n}));\r\n```\r\n\r\nThis is the data I will use in the doc:\r\n\r\n\r\n### Loading from an array ###\r\nFinaly, you can load the data from an array:\r\n```\r\n// Data out of MongoDB:\r\nvar data = [12,16,14,13,11,10,9,11,23,...];\r\n\r\n// Load the data\r\nvar t = new timeseries.main(timeseries.adapter.fromArray(data));\r\n```\r\n\r\n### Chaining ###\r\nYou can chain the methods. For example, you can calculate the moving average, then apply a Linear Weighted Moving Average on top of the first Moving Average:\r\n\r\n`t.ma().lwma();`\r\n\r\n### Getting the data ###\r\nWhen you are done processing the data, you can get the processed timeseries using `output()`:\r\n\r\n`var processed = t.ma().output();`\r\n\r\n### Charting ###\r\n#### Charting the current buffer ####\r\nYou can plot your data using Google Static Image Chart, as simply as calling the `chart()` method:\r\n\r\n```\r\nvar chart_url = t.ma({period: 14}).chart();\r\n// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:JDOLhghn0s92xuilnptvxz1110zzzyyvrlgZUPMHA&chco=76a4fb&chm=&chds=63.13,70.78&chxr=0,63.13,70.78,10\r\n```\r\n\r\n\r\n#### Charting the original data ####\r\nYou can include the original data in your chart:\r\n```\r\nvar chart_url = t.ma({period: 14}).chart({main:true});\r\n// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:ebgfqpqtzv40yxrstuwxyz000zzzzyyxvsqmjhfdZ,ebgfqpqtzv40yxvrw740914wswyupqdgPRNOXYLAB&chco=76a4fb,ac7cc7&chm=&chds=56.75,72.03&chxr=0,56.75,72.03,10\r\n```\r\n\r\n\r\n#### Charting more data ####\r\nYou can chart more than one dataset, using the `save()` method. You can use the `reset()` method to reset the buffer.\r\n\r\n`save()` will save a copy the current buffer and add it to the list of datasets to chart.\r\n\r\n`reset()` will reset the buffer back to its original data.\r\n\r\n```\r\n// Chart the Moving Average and a Linear Weighted Moving Average on on the same chart, in addition to the original data:\r\nvar chart_url = t.ma({period: 8}).save('moving average').reset().lwma({period:8}).save('LWMA').chart({main:true});\r\n// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:ebgfqpqthjnptuwyzyzyxyy024211yxusrojfbWUQ,ebgfqpqtzv40yxvrw740914wswyupqdgPRNOXYLAB,ebgfqpqtknqtvwxyxxyyy0022200zwvrpmidZXVTP,ebgfqpqthjnptuwyzyzyxyy024211yxusrojfbWUQ&chco=76a4fb,9190e1,ac7cc7,c667ad&chm=&chds=56.75,72.03&chxr=0,56.75,72.03,10\r\n```\r\n\r\n\r\n## Stats ##\r\nYou can obtain stats about your data. The stats will be calculated based on the current buffer.\r\n\r\n#### Min ####\r\n`var min = t.min(); // 56.75`\r\n\r\n#### Max ####\r\n`var max = t.max(); // 72.03`\r\n\r\n#### Mean (Avegare) ####\r\n`var mean = t.mean(); // 66.34024390243898`\r\n\r\n#### Standard Deviation ####\r\n`var stdev = t.stdev(); // 3.994277911972647`\r\n\r\n\r\n## Smoothing ##\r\nThere are a few smoothing options implemented:\r\n\r\n#### Moving Average ####\r\n```\r\nt.ma({\r\n period: 6\r\n});\r\n```\r\n\r\n\r\n#### Linear Weighted Moving Average ####\r\n```\r\nt.lwma({\r\n period: 6\r\n});\r\n```\r\n\r\n\r\n#### John Ehlers iTrend ####\r\nCreated by John Ehlers to smooth noisy data without lag. `alpha` must be between 0 and 1.\r\n```\r\nt.dsp_itrend({\r\n alpha: 0.7\r\n});\r\n```\r\n\r\n\r\n## Noise Removal ##\r\nMost smoothing algorithms induce lag in the data. Algorithms like Ehler's iTrend algorithm has no lag, but won't be able to perform really well on a really noisy dataset as you can see in the example above.\r\n\r\nFor that reason, this package has a set of lagless noise-removal and noise-separation algorithms.\r\n\r\n#### Noise removal ####\r\n```\r\nt.smoother({\r\n period: 10\r\n});\r\n```\r\n\r\n\r\n#### Noise separation ####\r\nYou can extract the noise from the signal.\r\n```\r\nt.smoother({period:10}).noiseData();\r\n// Here, we add a line on y=0, and we don't display the orignal data.\r\nvar chart_url = t.chart({main:false, lines:[0]})\r\n```\r\n\r\n\r\nYou can also smooth the noise, to attempt to find patterns:\r\n```\r\nt.smoother({period:10}).noiseData().smoother({period:5});\r\n```\r\n\r\n\r\n\r\n\r\n## Forecasting ##\r\nThis package allows you to easily forecast future values by calculating the Auto-Regression (AR) coefficients for your data.\r\n\r\nThe AR coefficients can be calculated using both the **Least Square** and using the **Max Entropy** methods.\r\n\r\nBoth methods have a `degree` parameter that let you define what AR degree you wish to calculate. The default is 5.\r\n\r\n*Both methods were ported to Javascript for this package from [Paul Bourke's C code](http://paulbourke.net/miscellaneous/ar/). Credit to Alex Sergejew, Nick Hawthorn and Rainer Hegger for the original code of the Max Entropy method. Credit to Rainer Hegger for the original code of the Least Square method.*\r\n\r\n#### Calculating the AR coefficients ####\r\nLet's generate a simple sin wave:\r\n```\r\nvar t \t= new ts.main(ts.adapter.sin({cycles:4}));\r\n```\r\n\r\n\r\n\r\nNow we get the coefficients (default: degree 5) using the Max Entropy method:\r\n```\r\nvar coeffs = t.ARMaxEntropy();\r\n/* returns:\r\n[\r\n -4.996911311490191,\r\n 9.990105570823655,\r\n -9.988844272139962,\r\n 4.995018589153196,\r\n -0.9993685753936928\r\n]\r\n*/\r\n```\r\n\r\nNow let's calculate the coefficents using the Least Square method:\r\n```\r\nvar coeffs = t.ARLeastSquare();\r\n/* returns:\r\n[\r\n -0.1330958776419982,\r\n 1.1764459735164208,\r\n 1.3790630711914558,\r\n -0.7736249950234015,\r\n -0.6559429479401289\r\n]\r\n*/\r\n```\r\n\r\nTo specify the degree:\r\n```\r\nvar coeffs = t.ARMaxEntropy({degree: 3}); // Max Entropy method, degree 3\r\nvar coeffs = t.ARLeastSquare({degree: 7}); // Least Square method, degree 7.\r\n```\r\n\r\n\r\nNow, calculating the AR coefficients of the entire dataset might not be really useful for any type of real-life use.\r\nYou can specify what data you want to use to calculate the AR coefficients, allowing to use only a subset of your dataset using the `data` parameter:\r\n```\r\n// We'll use only the first 10 datapoints of the current data\r\nvar coeffs = t.ARMaxEntropy({\r\n data: t.data.slice(0, 10)\r\n});\r\n/* returns:\r\n[\r\n -4.728362307674655,\r\n 9.12909005456654,\r\n -9.002790480535127,\r\n 4.536763868018368,\r\n -0.9347010551658372\r\n]\r\n*/\r\n```\r\n\r\n\r\n#### Calculating the forecasted value ####\r\nNow that we know how to calculate the AR coefficients, let's see how we can forecast a future value.\r\n\r\nFor this example, we are going to forecast the value of the 11th datapoint's value, based on the first 10 datapoints' values. We'll keep using the same sin wave.\r\n\r\n```\r\n// The sin wave\r\nvar t \t= new ts.main(ts.adapter.sin({cycles:4}));\r\n\r\n// We're going to forecast the 11th datapoint\r\nvar forecastDatapoint\t= 11;\t\r\n\r\n// We calculate the AR coefficients of the 10 previous points\r\nvar coeffs = t.ARMaxEntropy({\r\n\tdata:\tt.data.slice(0,10)\r\n});\r\n\r\n// Output the coefficients to the console\r\nconsole.log(coeffs);\r\n\r\n// Now, we calculate the forecasted value of that 11th datapoint using the AR coefficients:\r\nvar forecast\t= 0;\t// Init the value at 0.\r\nfor (var i=0;i<coeffs.length;i++) {\t// Loop through the coefficients\r\n\tforecast -= t.data[10-i][1]*coeffs[i];\r\n\t// Explanation for that line:\r\n\t// t.data contains the current dataset, which is in the format [ [date, value], [date,value], ... ]\r\n\t// For each coefficient, we substract from \"forecast\" the value of the \"N - x\" datapoint's value, multiplicated by the coefficient, where N is the last known datapoint value, and x is the coefficient's index.\r\n}\r\nconsole.log(\"forecast\",forecast);\r\n// Output: 92.7237232432106\r\n```\r\n\r\nBased on the value of the first 10 datapoints of the sin wave, out forecast indicates the 11th value should be around 92.72 so let's check that visually. I've re-generated the same sin wave, adding a red dot on the 11th point:\r\n\r\n\r\nAs we can see on the chart, the 11th datapoint's value seems to be around 92, as was forecasted.\r\n\r\n\r\n#### Forecast accuracy ####\r\nIn order to check the forecast accuracy on more complex data, you can access the `sliding_regression_forecast` method, which will use a sliding window to forecast all of the datapoints in your dataset, one by one. You can then chart this forecast and compare it t the original data.\r\n\r\nFirst, let's generate a dataset that is a little bit more complex data than a regular sin wave. We'll increase the sin wave's frequency over time using the `inertia` parameter to control the increase:\r\n\r\n```\r\nvar t \t= new ts.main(ts.adapter.sin({cycles:10, inertia:0.2}));\r\n```\r\n\r\n\r\n\r\nNow, we generate the sliding window forecast on the data, and chart the results:\r\n```\r\n// Our sin wave with its frequency increase\r\nvar t \t= new ts.main(ts.adapter.sin({cycles:10, inertia:0.2}));\r\n// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)\r\n// The default method used is Max Entropy\r\nt.sliding_regression_forecast({sample:20, degree: 5});\r\n// Now we chart the results, comparing the the original data.\r\n// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:\r\nvar chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});\r\n```\r\n\r\nAnd here is the result:\r\n\r\n* The red line is the original data.\r\n* The blue line is the forecasted data.\r\n* The red dot indicate at which point the forecast starts.\r\n\r\n\r\n\r\nDespite the frequency rising with time, the forecast is still pretty accurate. For the first 2 cycles, we can barely see the difference between the original data and the forecasted data.\r\n\r\n\r\nNow, let's try on a more complex data.\r\n\r\nWee're going to generate a dataset using 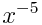, with a frequency increasing with time.\r\n\r\n```\r\nvar t \t= new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));\r\n```\r\n\r\n\r\nNow we forecast the same way we did in the previous example on the sin wave:\r\n\r\n```\r\nvar t = new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));\r\n// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)\r\n// The default method used is Max Entropy\r\nt.sliding_regression_forecast({sample:20, degree: 5});\r\n// Now we chart the results, comparing the the original data.\r\n// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:\r\nvar chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});\r\n```\r\n\r\n\r\n\r\nNow let's try the same thing, using the Least Square method rather than the default Max Entropy method:\r\n\r\n```\r\nvar t = new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));\r\n// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)\r\n// The default method used is Max Entropy\r\nt.sliding_regression_forecast({sample:20, degree: 5, method: 'ARLeastSquare'});\r\n// Now we chart the results, comparing the the original data.\r\n// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:\r\nvar chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});\r\n```\r\n\r\n\r\n\r\nNow, let's try the forecasting on real data, using the stock price of Facebook ($FB):\r\n```\r\n// We fetch the financial data from MongoDB, then use adapter.fromDB() to load that data\r\nvar t \t= new ts.main(ts.adapter.fromDB(financial_data));\r\n// Now we remove the noise from the data and save that noiseless data so we can display it on the chart\r\nt.smoother({period:4}).save('smoothed');\r\n// Now that the data is without noise, we use the sliding window forecasting\r\nt.sliding_regression_forecast({sample:20, degree: 5});\r\n/ Now we chart the data, including the original financial data (purple), the noiseless data (pink), and the forecast (blue)\r\nvar chart_url = t.chart({main:true,points:[{color:'ff0000',point:20,serie:0}]});\r\n```\r\n\r\n\r\n\r\n#### Forecasting optimization ####\r\nExploring which degree to use, which method to use (Least Square or Max Entropy) and which sample size to use is time consumming, and you might not find the best settings by yourself.\r\n\r\nThats why there is a method that will incrementally search for the best settings, that will lead to the lowest MSE.\r\n\r\nWe'll use the $FB chart again, with its noise removed.\r\n\r\n```\r\n// We fetch the financial data from MongoDB, then use adapter.fromDB() to load that data\r\nvar t = new ts.main(ts.adapter.fromDB(financial_data));\r\n\r\n// Now we remove the noise from the data and save that noiseless data so we can display it on the chart\r\nt.smoother({period:4}).save('smoothed');\r\n\r\n// Find the best settings for the forecasting:\r\nvar bestSettings = t.regression_forecast_optimize(); // returns { MSE: 0.05086675645862624, method: 'ARMaxEntropy', degree: 4, sample: 20 }\r\n\r\n// Apply those settings to forecast the n+1 value\r\nt.sliding_regression_forecast({\r\n\tsample:\t\tbestSettings.sample,\r\n\tdegree: \tbestSettings.degree,\r\n\tmethod: \tbestSettings.method\r\n});\r\n\r\n// Chart the data, with a red dot where the forecasting starts\r\nvar chart_url = t.chart({main:false,points:[{color:'ff0000',point:bestSettings.sample,serie:0}]});\r\n```\r\n\r\n\r\n\r\n\r\n## License ##\r\ntimeseries-analysis is free for non-commercial use under the [Creative Commons Attribution-NonCommercial 3.0 License](http://creativecommons.org/licenses/by-nc/3.0/legalcode). You are also allowed to edit the source code that is included along with the download. If you are a non-profit, student or an educational institute, feel free to download and use it in your projects.",
"_id": "timeseries-transform@1.0.2",
"scripts": {},
"_shasum": "7925da6112944d5c2b4b70a4a3b2869183f956f9",
"_from": "timeseries-transform@latest"
}