oi-wiki/docs/misc/hill-climbing.md

wiki for OI / ACM-ICPC

## 简介

爬山算法是一种局部择优的方法，采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。

* * *

## 实现

爬山算法每次在当前找到的最优方案 $x$ 附近寻找一个新方案（一般随机差值）。如果这个新的解 $x'$ 更优，那么转移到 $x'$ 否则不变。

这种算法对于单峰函数显然可行（你都知道是单峰函数了为什么不三分呢）。

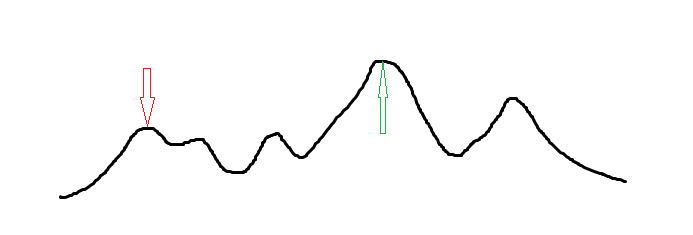
但是对于多数需要求解的函数中，爬山算法很容易进入一个局部最优解，如下图（最优解为 $\color{green}{\Uparrow}$，而爬山算法可能找到的最优解为 $\color{red}{\Downarrow}$）。

![](https://s1.ax1x.com/2018/08/22/PooS9e.png)

* * *

## 代码

此处代码以 [「BZOJ 3680」吊打 XXX](https://www.lydsy.com/JudgeOnline/problem.php?id=3680)（求 $n$ 个点的带权类费马点）为例。

```cpp
#include <cstdio>
#include <cmath>
const int N=10005;
int n,x[N],y[N],w[N];
double ansx,ansy;
void hillclimb() {
	double t=1000;
	while(t>1e-8) {
		double nowx=0,nowy=0;
		for(int i=1;i<=n;++i) {
			double dx=x[i]-ansx,dy=y[i]-ansy;
			double dis=sqrt(dx*dx+dy*dy);
			nowx+=(x[i]-ansx)*w[i]/dis;
			nowy+=(y[i]-ansy)*w[i]/dis;
		}
		ansx+=nowx*t,ansy+=nowy*t;
		if(t>0.5) t*=0.5; else t*=0.97;
	}
}
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;++i) {
		scanf("%d%d%d",&x[i],&y[i],&w[i]);
		ansx+=x[i],ansy+=y[i];
	}
	ansx/=n,ansy/=n;
	hillclimb();
	printf("%.3lf %.3lf\n",ansx,ansy);
	return 0;
}
```

* * *

## 劣势

其实爬山算法的劣势上文已经提及：它容易陷入一个局部最优解。当目标函数不是单峰函数时，这个劣势是致命的。因此我们要引进 [**模拟退火**](https://oi-wiki.org/misc/simulated-annealing/)。